Волчок Сакаи, иначе волчок из скрепки, был придуман в 1986 году японским профессором физиком Такао Сакаи из университета Тохоку в Сэндай. Профессор хотел продемонстрировать своим студентам возможность создания реально функционирующего волчка из подручного материала, например, из обыкновенной канцелярской скрепки.
А чем мы хуже профессора и его учеников?
Чуть-чуть терпения, пара испорченных скрепок, и Вы - обладатель волчка! Можно сказать просто и ласково «волчок», а можно важно и по-научному - «гироскоп».
- Выбираем скрепку из достаточно гибкого металла.
- Сначала скрепочку выпрямляем, а затем начинаем гнуть …
- Концы проволоки скрепки становятся осью вращения, а середина скрепки, образуя окружность, превращается в маховик.

Вот тут-то и начинаются хитрости ...
А самая главная - центр тяжести конструкции должен лежать на оси вращения волчка.
А как же для этого надо изогнуть проволочку?
Для того, чтобы получить максимальный момент инерции, надо согнуть колечко маховика как можно большего радиуса. Если согнуть из скрепки полную окружность, то за счет участков проволоки, соединяющей окружность с осью вращения, центр тяжести волчка сместится с оси вращения. Как рассчитал профессор Сакаи, окружность не должна быть полностью замкнутой, открытый угол β должен составлять, если точно, то 53,13°.
А как доказать, что непременно 53,13°?
Делаем расчет!
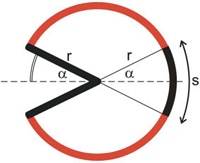
Если открытый угол β будет больше или меньше указанного, то центр тяжести волчка не будет совпадать с центром окружности проволочного маховика. При расчете нужной величины открытого угла β достаточно принять во внимание только участок открытого угла β и лежащую противоположно ему (и соответствующую вертикальному углу) часть дуги окружности. Остальные участки окружности, лежащие симметрично относительно центра окружности и отмеченные красным цветом, можно при расчете не рассматривать. Введем обозначение половины открытого угла β, как α .
На следующем рисунке введем систему координат и расположим начало координат в центре окружности. Обозначим расстояние центра тяжести участка проволочки, образующей дугу, от начала координат величиной x1. Пусть длина проволочной дуги в пределах заданного угла β равна s.
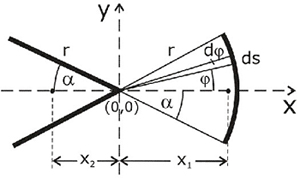
Тогда координату центра тяжести можно вычислить, учитывая симметричность центра тяжести относительно координатной оси х, с помощью линейного интеграла:
x1 = ∫x ds/s = 2rrsin α /s
Если обозначить р - плотность материала проволоки, А - поперечное сечение проволоки, тогда масса участка дуги составит m1 = spA . Относительно начала координат участок данной дуги создает вращающий момент M1 = m1x1 = 2rrpA sinα.
Центр тяжести участка проволоки, образующей открытый угол β, лежит на расстоянии х2 = r/2 cos α от начала координат, а масса составляет m2 = 2rpA. Создаваемый этим участком вращающий момент относительно начала координат имеет величину M2 = m2⋅x2 = rr⋅cosα•p•A. После приравнивания моментов М1 и М2 получаем tang α = 0,5 и, следовательно, α = 26,565°. Таким образом, открытый угол β = 2α = 53,13°. Но нам придется этот угол наметить приблизительно, поэтому, делая волчок, возможно, Вы испортите не одну скрепку!
Но, ведь ради науки нам с вами скрепок не жалко?


